This article concerns the generation of simple diagrams containing a series of interconnected nodes. Often, simple diagrams such as these can add a new dimension of usability to a data-driven application. For example, you can:
- Show the connections between related entities (e.g. people and relationships)
- Visualise complex structures (e.g. tree data structures)
- Follow logic flows and sequences (e.g. flow charts)
- Produce a navigation map (e.g. for a website)
An ever-present challenge in dynamically-generating diagrams, however, is the layout of the nodes. Aesthetics dictate the need for uniform spacing between nodes, radial distribution and minimal crossing of lines (among other things), yet these are very difficult to achieve using ‘blind’ techniques (rule-based layouts and other algorithms that position nodes without considering the overall diagram).
Force-directed algorithms present an exciting solution to this problem. Here, simple mechanical forces are applied to the diagram (essentially by running a physics simulation), resulting in a layout that exhibits the properties of emergent complexity. The appropriate selection of forces and formulae are capable of producing layouts that meet the aesthetic goals outlined above. In their purest form, force-directed algorithms balance the forces of charged-particle repulsion between each node (Coulomb’s Law) and spring attraction between each pair of connected nodes (Hooke’s Law). After a number of iterations (each representing a slice of time during which the forces act upon the nodes), an equilibrium is reached and the layout process is complete.
I have implemented a force-based layout algorithm in C# and GDI+. It provides a simple Diagram class which acts as a container for descendants of the Node abstract class. The structure and layout of the diagram is separated from the rendering, which is fully overridable. The implementation is not tied to Windows Forms, but is fully compatible, so diagrams can either be drawn onto a System.Windows.Forms.Control (for display and interactivity) or directly onto a System.Drawing.Bitmap (for exporting).
Classes
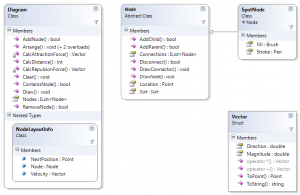
Node
Node is the base class for a node on the diagram. Conceptually, it has a Location on the cartesian plane and a series of Connections to other nodes on the diagram. It also makes provision for a Size (used when rendering) and abstract functionality for drawing both the node and its (child) connections. Connections between nodes can be hierarchical (parent-child) or two-way. If a diagram contains a mixture of different derived types, parent nodes are responsible for drawing the connections to their children (although a base implementation is provided).
SpotNode is an example concrete implementation of Node that has additional visual properties and contains logic to draw itself as an 8×8 circle.
Diagram
Diagram serves as both a collection of Node objects and the layout provider. The implementation of the force-directed algorithm resides in this class. Although it performs no painting itself, it provides a Draw() method that scales the diagram to match a drawing surface and instructs each node to draw in the correct bounds.
It also defines a nested class, NodeLayoutInfo, which tracks the mechanical properties (velocity, future coordinates) of each node during the force-based simulation.
Vector
I developed the Vector structure as part of an earlier project. It models (on a basic level) a vector whose Magnitude and Direction are System.Double, with the direction expressed in degrees. It uses operator overloading to support vector addition and scalar multiplication. In the force-based algorithm, it is necessary to calculate and express the forces acting on each node in terms of both magnitude and direction, hence a vector representation is desirable.
The Layout Algorithm
At the heart of the force-directed algorithm are the methods that calculate the forces themselves:
The repulsion force is exerted by every node in the diagram, and each node is repelled (however slightly) by every other node in the diagram. This force is likened to the repulsion of charged particles, and so it is based on Coulomb’s Law; F = k(Q1Q2/r2) – where k is a constant, Q is the charge and r is the distance between the particles. Since all of our nodes are equivalent, we can ignore the charge term. In other words, as the distance between the nodes increases, the repulsion force decreases quadratically. This calculation is performed in the CalcRepulsionForce() method:
private Vector CalcRepulsionForce(Node x, Node y) {
int proximity = Math.Max(CalcDistance(x.Location, y.Location), 1);
double force = -(REPULSION_CONSTANT / Math.Pow(proximity, 2));
double angle = GetBearingAngle(x.Location, y.Location);
return new Vector(force, angle);
}
The attraction force is exerted on each node by the nodes that are connected to it; isolated nodes are therefore unaffected by this force. The connectors between the nodes are regarded as spring-like, hence the force calculated using Hooke’s Law; F = −kx – where k is a constant and x is the difference between the length of the spring and the distance between the nodes (i.e. the extension of the spring). In other words, as the distance between the nodes increases, the force pulling them back together increases proportionally (at least until the spring is fully relaxed, in which case the force stops applying). This calculation is performed in the CalcAttractionForce() method:
private Vector CalcAttractionForce(Node x, Node y, double springLength) {
int proximity = Math.Max(CalcDistance(x.Location, y.Location), 1);
double force = ATTRACTION_CONSTANT * Math.Max(proximity - springLength, 0);
double angle = GetBearingAngle(x.Location, y.Location);
return new Vector(force, angle);
}
The force-directed algorithm applies these forces to the nodes via an iterative simulation, as follows:
- Randomise the initial coordinates of each Node – even a tiny variation will be sufficient.
- Until the maximum number of iterations is exceeded (or the stop condition is satisfied):
- Initialise the totalDisplacement to zero.
- For each node:
- Initialise the netForce Vector to zero.
- Call CalcRepulsionForce() on every other node in the diagram, adding the result to netForce.
- Call CalcAttractionForce() on every node connected to the current node, adding the result to netForce.
- Add netForce to the node’s velocity vector.
- Let the node’s new position be set to the vector sum of its current position and its velocity.
- For each node:
- Calculate the displacement caused by moving the node to its new position, adding the result to totalDisplacement.
- Move the node to its new position.
- If totalDisplacement is less than a threshold value, trigger the stop condition.
- Offset each node such that the diagram is centered around the origin (0,0). (During iteration, the diagram may creep.)
Usage Examples
Drawing a basic diagram to a bitmap
Diagram diagram = new Diagram();
// create some nodes
Node fruit = new SpotNode();
Node vegetables = new SpotNode();
Node apple = new SpotNode(Color.Green);
Node orange = new SpotNode(Color.Orange);
Node tomato = new SpotNode(Color.Red);
Node carrot = new SpotNode(Color.OrangeRed);
diagram.AddNode(fruit);
diagram.AddNode(vegetables);
// create connections between nodes
fruit.AddChild(apple);
fruit.AddChild(orange);
fruit.AddChild(tomato);
vegetables.AddChild(tomato);
vegetables.AddChild(carrot);
// run the force-directed algorithm
diagram.Arrange();
// draw to a Bitmap and save
Bitmap bitmap = new Bitmap(640, 480);
Graphics g = Graphics.FromImage(bitmap);
diagram.Draw(g, new Rectangle(Point.Empty, bitmap.Size));
bitmap.Save("demo.bmp");
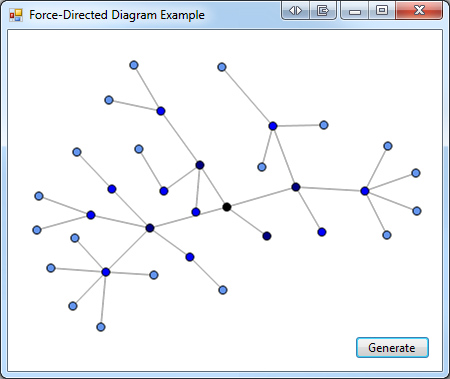
Sample application
In the source code package (at the bottom of the article), I have included a simple Windows Forms application that demonstrates how to generate a random hierarchical diagram and paint it persistently on a Form. The layout is performed in a separate thread, and can optionally be displayed in a real-time, animated fashion.
Final Words
Force-directed algorithms are not perfect when it comes to arranging the nodes on a diagram; they are subject to conforming to local extremes rather than finding a 100%-optimal layout. This means that diagrams with a large number of nodes will typically have a higher occurrence of crossed lines. However, even when a less-optimal result is obtained, said result is often still visually striking. Running time can be a problem with particularly dense diagrams, but as already discussed, simpler diagrams produce a more aesthetically-pleasing result anyway. In most practical applications, a force-based approach provides a very good result for dynamically-generated diagrams.
With respect to my implementation, it is a very bare-bones approach, but it is also very scalable; for example, if appropriate node subclasses were written, it could be used to produce flow-charts, people-relationship diagrams, site maps for websites, brainstorming charts or even database diagrams (with some additional functionality). The ability to automatically generate such diagrams can open up a whole new world in terms of application usability, data analysis and the production of deliverables.
A force-directed algorithm will definitely drive my future diagramming/graphing projects.
Download
If you find my code useful, please consider making a donation.
ForceDirected.zip – rev 1 (source code and example application)
- 2013/02/24 – Improved Vector class by replacing Math.Tanh() approach with Math.Atan2()
Vector.zip (drop-in replacement for the Vector class above)
- 2015/02/28 – Added an alternative Vector implementation that produces a ~33% performance boost

😛 it is very useful
ForceDirected.zip seems to be corrupt and cannot be opened 🙁
The download is working fine from my end. Opens and extracts successfully in both Windows Explorer and WinRAR – what program are you trying to open it with?
Trying to open it with windows explorer. Says file is invalid.
I’ve downloaded it several times, same error every time.
I’ll see if I can find another utility to try.
Okay, curious problem here – downloads fine on Firefox, fails on IE. The file saved from IE is missing the header, the one saved from Firefox is complete. Sounds like a problem with my web host.
It will work if you use Firefox, alternatively i’ll be happy to e-mail you the working ZIP file.
That’s pretty strange. I would be grateful if you could email it to me.
Thanks!!!
Great program.
I have managed to implement it. I do have one question though: when running the program is there a way to prevent the nodes disappearing off the screen when the algorithm starts. It only seems do do it when there are a lot of nodes and i cant seem to figure out how to always make the nodes central to paint screen.
Also have you had a look at and what are your views on this program and how it differs to yours?
http://antimatroid.wordpress.com/2010/05/01/tree-drawing-force-based-algorithm/
Thanks
Thanks, Eaxrl1 🙂
Due to the initial, random placement of the nodes when the algorithm starts, the first few cycles of the simulation result in very rapid movements as the forces compete and begin to reach equilibrium; it’s natural for clusters of nodes to push away from the rest of the diagram during this initial phase, since the forces acting on them are greater than on the others.
There are a few solutions you could look at. You could change the initial placement of the nodes so they follow a more uniform distribution. For diagrams with large numbers of nodes, you could increase the spacing between them (by increasing the bounds that the random placements are restricted to). You could also look at modifying the constants for attraction, repulsion, damping and spring length – the default values I provided are optimised for diagrams with a smaller number of nodes. Finally, you could simply shift the rendering origin each time you display the diagram – in my implementation, this is done only after the layout is finished, but it could be done after each iteration.
The link you provided shows an implementation that is not all that different to mine. The underlying principles are certainly the same, and his videos simply show what I described earlier; with a shifting origin during rendering. He’s confined himself to the simple case where he’s only drawing trees; more complex diagrams are possible (with both implementations, if some tweaking were done), where each node could be connected to several other nodes. But, yeah, a very similar implementation.
Cheers Bradley,
I will have a go at shifting the rendering origin if i can figure out how. I am very new to programming so learning as i go. I am using the force-directed algorithm concept as part of a much bigger program of random discontinuous fibres embedded in a cell (think loft insulation or textile materials). So your program is very useful, got a long way to go though.
Thanks
That sounds like quite an exciting application for the algorithm; using it for its basis in physics rather than simply taking advantage of the physics for more mundane purposes 🙂
You can center the origin during each iteration by making one simple change to the Arrange() method in the Diagram class; you just need to move this block of code (at the bottom of the method):
// center the diagram around the origin
Rectangle logicalBounds = GetDiagramBounds();
Point midPoint = new Point(logicalBounds.X + (logicalBounds.Width / 2), logicalBounds.Y + (logicalBounds.Height / 2));
foreach (Node node in mNodes) {
node.Location -= (Size)midPoint;
}
…into the loop immediately above it (just before the exit conditions).
Ha, well that was simple, now i feel a bit dense.
Once again thanks i would have ended up spending a lot of time figuring it out. If i manage to get the program working i will upload a video. Thanks
I had a go with your source in ANIMATE mode and was a bit curious why the graphs all seem to move towards the top left then back to the center, when there is no initial momentum in the system to make things move (on average) at all. I reviewed the code and found that you are consistently using the Math.Tanh method (hyperbolic tanget), where you really need to be using Math.Atan (arc tangent) or better yet Math.Atan2 so you can remove all of the angle range checks. Upon making these changes, the graphs almost always stay in the visible area of the canvas and the center of gravity stays near the middle. The final layouts also seem more intuitive (to me anyway), considering the forces you are modelling.
Really nice work – I’ve always had a desire to play with force-directed placement and your project is a great starting point. I’ve begun to add some simulated-annealing effects to solve the local minimum issue that often arise in systems like these.
Thanks a lot for the tips – it’s always great to get feedback from someone who is a little stronger in their mathematics than I am 🙂 I’m quite curious to implement those changes and see the results for myself!
Many thanks for this post! it is very useful to understand concept of layout arrangments. Agree with Bradley Smith :))
How can we handle nodes of various sizes?
For the purpose of the simulation, all nodes are regarded as point sources rather than considering their size or shape. For circular nodes, all you have to do is set the scaling factor accordingly. There is no easy way to handle oblong or rectangular nodes without introducing some potential overlap.
With a very large number of nodes I wanted to see the layout zoomed. Possibly adding some scroll bars.
I set the diagram bounds large and as expected the diagram is centred off the viewport, but unexpectedly it does not seem to draw almost to the edges of the supplied bounds as it does if one provides bounds the same or a little smaller than the viewport. Consequently it is not as zoomed as one would like, but is about the same size on a very large canvas so to speak.
Do you know the reason for this? Is there perhaps a built in maximum size for the diagram? Is the bounds for each node set according to the available diagram bounds or perhaps based on the number of nodes?
Is there a way to resolve this?
My best guess is that this is due to the diagram scaling not taking into account the size of the nodes themselves, only the bounds of the connectors. You would need to modify the GetDiagramBounds() method to consider the size of each node.
The code provided is intended to be a proof-of-concept only; features like a scrollable viewport are fairly easy to implement on top of the existing code. You simply draw the diagram with larger bounds and clip to the bounds of the viewport when displaying it.
Hi Bradley,
great work and many thanks for uploading your work.
I’ve been studying it a bit and came to some conclusions that I cannot really explain.
First of all, I needed the algorithm to produce graphs that intersect very rarely, possibly never.
With your constants and a random graph that produced more than 40-50 nodes it often intersects.
This might seem odd, but changing the constants like this:
private const double ATTRACTION_CONSTANT = 0.3; // spring constant
private const double REPULSION_CONSTANT = 400; // charge constant
private const double DEFAULT_DAMPING = 0.85;
private const int DEFAULT_SPRING_LENGTH = 200;
private const int DEFAULT_MAX_ITERATIONS = 100;
and in the CalcRepulsionForce method changing the Coulomb’s Law
from: -(REPULSION_CONSTANT / Math.Pow(proximity, 2))
to: -REPULSION_CONSTANT/proximity
I noticed a significant improvement in avoiding intersections.
There is some clustering side effect in the nodes that are in the end of branches, but that I don’t mind. Also, significantly less iteration is needed to get the wanted result.
There is an obvious connection between the REPULSION_CONSTANT and proximity, but I haven’t been able to set the constant to achieve a similar result as with changing the Coulomb’s Law. Not squaring the proximity is significant only to the first few iterations, as the number of iterations grow, it can be changed back to original square.
Do you have any idea why the algorithm appears to work better with these changes and is there something else that I’m missing? I am a computer science student and I would really appreciate your help if you have some opinions about this topic.
In addition, I included some pictures of graphs that I created using the initial settings and my settings:
http://imageshack.us/photo/my-images/836/example1a.png/
http://imageshack.us/photo/my-images/42/example1b.png/
http://imageshack.us/photo/my-images/255/example2a.png/
http://imageshack.us/photo/my-images/267/example2b.png/
http://imageshack.us/photo/my-images/818/example4a.png/
http://imageshack.us/photo/my-images/571/example4b.png/
Hi, your findings are rather interesting! The spring and charge constants provided in my example are certainly not the optimal values; in some respects, the ideal values for these constants depend upon the scale and complexity you are using for the nodes of the diagram. However, once you’ve found the optimal settings for a given type of diagram, these values should remain constant. The damping and spring length can (and probably should) vary for individual diagrams; they are intended to be variables in the equation.
The problem with changing the way that repulsion is calculated is that the forces are no longer properly balanced. Repulsion is supposed to follow the inverse square law, and by making it a linear relationship, nodes which are very far apart are more likely to influence each other. Now, this may be desirable in certain circumstances; in this case, as a side-effect of the nodes repelling each other from a greater distance, they are more inclined to line up in such a way that they don’t intersect. This could create other problems, however, such as the bunching you observed (neighbouring nodes are having too great an effect on nearby clusters) and, in general, greater repulsion forces will lead to diagrams that are more (unnecessarily) spread-out.
You should be able to improve the layout of the nodes by tweaking just the constants (and leaving the force calculations alone) – you may have to increase/decrease them by several orders of magnitude to get a noticeable effect. The addition operator in the Vector class (as pointed out in comments on this post already) could benefit from the improved accuracy that the Math.Atan2 method offers (vs my Math.Tanh approach) – after changing the implementation, my results improved measuredly.
Once again, thanks for taking the time to explore the algorithm – I hope this goes some way to answering your questions.
Thank you for your answer, I’ll continue trying to adjust the constants.
I understand why it is wrong to change the laws of physics 🙂 but if I don’t succeed in adjusting, I will probably have to leave these changes and settle with the side-effects (which are acceptable for my problem domain). I will also consult with my professor.
Thank you again and continue the good work!
Marina, did you come up with the “right” or better constants to use?
Marina did you succeed?
Could you please post the source code after Math.Atan2 was used? Thanks
Updated the post with a new link. Sorry about the delay – i’ve been on vacation.
Thanks for this! I might be making a silly mental mistake here but it seems like you don’t need to calculate these angles at all. If you know your hypotenuse (i.e. your distance between your points) – you can get your x and y force component as: xForce = xDiff/dist * force and yForce = yDiff/dist*force. It seems that by converting to angle form and then getting back your rise and run by using atan then sin and cos you’re just using up lots of computation cycles and as noted above possibly introducing inaccuracies. I could be totally missing something though! Regardless a very helpful tutorial/demo.
All we have to work with are the magnitude and direction for each of the two vectors being added; these do not form right-angled triangles, so there is no hypotenuse. The only technique I know of to add vectors is to break them into their x and y components, add these together and then obtain the new magnitude (Pythagorus’ Theorem) and direction (arc tangent). If you know of a more efficient way to add vectors in terms of their magnitude and direction only, i’d be very happy if you shared it 🙂
Again, could be missing something but the idea is never to compute your vector (magnitude and angle) in the first place. For both the attraction and repulsion algorithms, for each node you compute the force between it and every other node, summing all of the xForces and yForces as you go. If point m is at (0,0) and point n is at (4,3), then distance between the two is sqrt(4^2 + 3^2) = 5. We can then do our force calculations and get the total force along this hypotenuse using the computed distance. Then, the x-component of that force should just be (4-0)/5 * force and the y-component should be (3-0)/5 * force. This should be equivalent to what I believe you’re doing, which is using atan to get the angle from rise over run (4/3), and then later demcomposing it before you add your vectors to get x – cos(theta) * force – and y – sin(theta) * force. But that’s just going in a circle right, as sin(atan(y/x)) * force = y/dist * force – where dist is the hypotenuse. You should never need to go to angle form in the first place. And although the two ways should be equivalent when doing something O(n^2) like this doing trig functions is hugely costly, not to mention possibly introducing inaccuracies as previously discussed.
Its also completely possible that I’m being stupid and missing something obvious. My trig is definitely a bit rusty!
You make a fair point. It may be worth investigating whether an x/y component representation results in faster computation times for the force-based algorithm (as a whole) compared to the magnitude/direction representation. It will still be necessary (or, at least, most convenient) to compute angles to determine the force vectors – but by making vector addition less costly, there could be a real difference in performance. I’ll make this the subject of a future article!
Bradley,
Still not sure why “It will still be necessary (or, at least, most convenient) to compute angles to determine the force vectors”. If you have everything separated into x and y components you can just sum all x forces and all y forces for a given node and then add xForce to xVelocity and yForce to yVelocity. Should never have to deal with angles at all.
When calculating the attraction and repulsion forces, it’s convenient to use the magnitude & direction representation; the magnitude of the force is based on the distance between two nodes and the direction is always the bearing from one node to another. The force calculations would be more complex if they were written in terms of X and Y components.
However, I have done some preliminary tests using an alternative Vector implementation that stores X and Y components instead of magnitude and direction; it offers a constructor which accepts magnitude and direction, to allow the force calculations to remain unchanged. This means that trig functions are only used when calculating the forces and not during vector addition. Using the demo application I included with this post, i’m seeing an approximate 33% performance boost using this approach – so I guess I have you to thank for that! 🙂
Hi Brad,
” i’m seeing an approximate 33% performance boost using this approach – so I guess I have you to thank for that! ”
Is it easy to implement the changes, to achieve the performance boost, to the rev1 code supplied with this article?
BTW thanks for the already great rev1 version with I just found and got running in LinqPad 🙂
Hi Peter,
I’ve updated the article – see Vector.zip in the Download section. This is a drop-in replacement for the old Vector class.
Hope this helps!
Hi Brad,
Many thanks for the fast response and the updated vector class.
It works and I can notice that the new code is a lot faster 🙂
I have found this very interesting. Do you have a version in Visual C++ (e.g. MFC)? How easy do you think it would be to port? Any tips?
I have not ported the code to C++ myself, but the force-based algorithm itself would not be difficult to implement in C++. The most complicated functionality to port would be the drawing/rendering code (since that is very API-dependant) – however, if you are a whiz with GDI+ or other common graphics APIs for C++, you should be fine.
I implemented a force diagram in CUDA (Nvidia’s Graphics Language), which is basically C++ (all the classes and such are standard C++). Its super fast, you can basically simulate millions of nodes in real time, and I’m going to try to make it scale to multiple GPUs. Currently it is coupled with a webserver, outputting JSON to be consumed by a webpage (for which I use processing.js to do the visualization). Eventually I’ll just use an OpenGL context to render 3D network graphs straight to screen, but that’s a bit in the future. I’m planning on building this into a full-fledged GPU-powered graph database, but I’ll put up a link to my github repository of the code soon (next week or two hopefully) which may be of use to you – since its basically all C++ (you could port the CUDA kernels to C++ with ease, since CUDA is basically a subset of C++).
Hello Bradley,
Thank you very much for uploading your work. I would like to know is it possible to reimplement your example in WPF? I am student, and my task is very similar to this, but I need to provide solution in WPF, which yet I don’t know very well.. Can you tell me your opinion about that, how complicated it would be?
I believe that it would be relatively simple to rework my implementation in WPF. The biggest difference is that WPF does not use GDI+ (System.Drawing namespace) for rendering, rather the functionality of its own System.Windows.Media and System.Windows.Imaging namespaces. Where GDI+ is a raster-based API, WPF is vector-based. While the current Draw() method is called every time the screen needs to be updated, drawing the diagram using a Graphics object, you would simply output a Drawing object containing various Geometry objects that represent the nodes (e.g. EllipseGeometry) and the connectors (e.g. LineGeometry). Once you assign this Drawing object to a Window (I believe they can be placed inside many different WPF elements; Image, Canvas, Panel, etc) the WPF engine will take care of drawing it for you.
There are equivalent types in the WPF namespaces for most (if not all) of the types used in my implementation – for example, the Point and Rectangle classes. Once you replace the GDI+ rendering code with equivalent WPF code, everything else in the algorithm remains the same; the calculation of forces, the vector mathematics, they are not dependant on the presentation layer. I do not have much experience with WPF myself, but I think this exercise would require very little effort indeed.
You may be interested to hear that I was particularly bored tonight, and so I decided to write a variation of my Force-Directed Diagram Layout Algorithm for use in WPF, including a sample application.
I’ve packaged it as a Visual Studio 2010 solution, available here.
Thank you Bradley! I am so happy right now.. this is exactly what I needed for my project.
Do you always coding when you get bored? 🙂
I wish you all the best!
Hi Bradley,
I have adjusted your sample in WPF to my project, but now I have new chalenges. I should implement that nodes can be movable along with incident edges using mouse dragging. It is recommended Canvas layout to be used, and I have a problem. Your drawing is Image type, so I don’t know how to put event handlers to it. 🙁
I tried to put drawing in Canvas container, and added following piece of code, but nothing happens. I suppose that I should use Location of nodes in Node.cs and Size of SpotNode, but I don’t know how to make it work, I am so confused now… Please help.
// stop dragging and release mouse capture
void Canvas_PreviewMouseLeftButtonUp(object sender, MouseButtonEventArgs e)
{
if (canv1.IsMouseCaptured)
{
IsDragging = false;
canv1.ReleaseMouseCapture();
e.Handled = true;
}
}
// Works out the delta for the mouse movement
void Canvas_PreviewMouseMove(object sender, MouseEventArgs e)
{
if (canv1.IsMouseCaptured)
{
//if dragging, get the delta and add it to selected
//element origin
if (IsDragging)
{
Point currentPosition = e.GetPosition(canv1);
double elementLeft = (currentPosition.X – startPoint.X) + selectedElementOrigins.X;
double elementTop = (currentPosition.Y – startPoint.Y) + selectedElementOrigins.Y;
Canvas.SetLeft(selectedElement, elementLeft);
Canvas.SetTop(selectedElement, elementTop);
}
}
}
// Obtain start point and selected element, and record
void Canvas_PreviewMouseLeftButtonDown(object sender,MouseButtonEventArgs e)
{
//Dont act apon events from parent element
if (e.Source == canv1)
return;
if (!IsDragging)
{
startPoint = e.GetPosition(canv1);
selectedElement = e.Source as UIElement;
canv1.CaptureMouse();
IsDragging = true;
selectedElementOrigins = new Point(Canvas.GetLeft(selectedElement), Canvas.GetTop(selectedElement));
}
e.Handled = true;
}
As WPF is not one of my strong points, I don’t feel qualified to answer your question. I wish you luck with it, though!
Sir,
can you please tell how to run your code in a C# compiler. I am new in C#
Hi, the easiest method is to extract the ZIP to your hard drive, open Visual Studio and select ‘New’ -> ‘Project from Existing Code’. Choose ‘Visual C#’ and browse to the folder containing the files. Select ‘Windows Application’ as the output type. After the wizard finishes, you should be able to compile the project without any issues.
Pingback: Using DENSE_RANK() to Build a Better Tag Cloud | Brad Smith's Coding Blog
Pingback: AI War Beta 6.044-6.045 “So That’s What A Vines Map Looks Like” Released! | cika
Pingback: AI War Beta 6.044-6.045 “So That’s What A Vines Map Looks Like” Released! | Arcen Games
Hi Brad, I put together a neat little program using your code and wanted to thank you for making this available, which saved me hours, not having to figure this stuff out myself. Here’s the article: Automating Semantic Mapping of a Document With Natural Language Processing which I think you’ll find as a really neat idea around your FDG implementation. Thanks again! — Marc
Thanks for the link, and for the attribution in your article 🙂 This seems like an ideal use for a force-directed graph, since the number and depth of nodes is dynamic and unpredictable. As well as providing visual interest in your app, it also presents the information in a manner that would be far less intuitive without a diagram. It’s always gratifying to see the concepts in my articles find a practical use in someone else’s work.
Thanks for making the info about force-directed diagrams so easy to understand. It really helped me to get a better grasp of the subject.
I modified the algorithm so that it only calculates for unique node-pair interactions and am getting a significant speed improvement. It should not be this fast. Any ideas why?
I have uploaded it to GitHub.
This seems like a very sensible way to improve the efficiency of the algorithm, thanks for sharing your code!
At first glance, I think the increase in performance is due to the reduced number of calculations per iteration, as well as the overall number of iterations. I think the total time taken to arrive at a solution would get a little closer to the 50% mark if you modified the fitness criteria to allow the algorithm to run for a comparable number of iterations (e.g. by lowering the minimum displacement constant). This will likely result in more optimal solutions as well. Give it a try and see if you can strike a better balance between speed and accuracy 🙂
Really incredible program, elegant, useful, & a bit fun to watch with the animations activated. 3 questions…
If a user was able to calculate the maximum depth of tree nodes or the highest single number of branches prior to generating the diagram, could these be used as parameters to determine a more ideal set of values for the constants?
If one were to use 3D points in a Viewport3D control, how would this impact the formulas used to simulate the charge & spring effects?
Also, is there a way to extend the node class to make each node a customized, selectable user interface element within a WPF control, (not just a drawn shape on a bitmap)? From a user’s perspective, it would be useful to add Tool Tips or a right-click context menu for each node to get information about items in a decision tree. It would also be a nice visual for users to be able to left-click highlight the path from the root through each parent node to the selected item, especially to clarify the path around intersections.
I haven’t experimented with tweaking the constants extensively, but I don’t think you will find any obvious correlation between the depth or number of branches and the individual constants. The spring and charge constants do not need to vary with the complexity of the diagram; they are just there to keep the forces in balance and the distances in the right order of magnitude. The spring length is just another modifier on those forces and probably only needs changing if your nodes are overlapping. In turn, damping only limits the amount of movement per iteration. The only real value that may vary with each individual diagram is the maximum number of iterations; more complex diagrams, particularly those with a higher potential for crossed lines, are likely to need more iterations to complete – but this is more about the number of connections per node, rather than the number/depth of nodes themselves. (e.g. a diagram in which each node connects to every other node will require many more iterations to complete than a diagram where each node connects to only 2 other nodes)
In 3D, you would need to use the vector forms of Coulomb’s Law and Hooke’s Law and calculate these using 3D vectors instead of the 2D vectors used in my project. In 3 dimensions, it’s no longer useful to use the ‘magnitude and direction’ representation and far easier to just use x, y and z components. I would have to brush up on my trigonometry before giving any more specific advice here.
The nodes in my project are intended just for drawing purposes, but the only thing you’d need to make them interactive would be a hit-test method (probably implemented on the diagram itself) – given a position on the diagram, you would iterate through the nodes until you found one whose bounds contained the point, then return that node. Once you have this functionality, it’s very easy to implement the event handling for MouseOver/MouseClick, etc.
Thanks for this greate example. I started to adapt the diagram- and node classes to use them in a MVVM Wpf application. The diaram is shown in a ScrollViewer control and I added a slider to change its scale for zooming in- and out.
In addition it is possible to relocate the nodes by dragging them with the mouse.
My question: Is it possible to define a min. distance between each nodes to prevent them from overlaping, for example 300px in the X Axis and 70px on Y?
At the end I will just align the width and height of my Canvas to the bounds of the diagram and enable the scrollbars if necessary.
Hi,
Is it possible to download a sample of your WPF implementation? I’m working on a similar project but also requires the Bing Map WPF Control. I’d love to see how you implemented Bradley’s codes in WPF.
Hi. Thanks for the code.
I have a noob question…. Can I get HTML and buttons in the nodes?
There’s no built-in support for them, but you could write your own class that extends Node; the rendering logic can be overridden as necessary. Getting nodes to respond to user interaction is a little more complicated, and would require you to do hit testing in response to mouse events.
Thanks Bradley. That sounds hard, but it’s good to know its possible. I may give it a try in the future.
Much appreciated
Is it possible to implement your app using Bing Map WPF Map Control? I would like to be able to use water management icons as nodes but add Location (latitude, longitude) for each node. Then use arrows for connectors to show the “direction” of water flow (which node flows into which node). WPF uses XAML and not sure if this one can be implemented using XAML.
Hi, I made an experimental version in WPF a while back, which you can download from here: https://www.brad-smith.info/blog/wp-content/uploads/2013/03/ForceDirectedWPF.zip
I don’t have much practical experience with WPF, however, so i’m not sure if it could be further extended to work with the Bing Map Control – but I do not see why it couldn’t be. This would need to be done in code-behind rather than XAML, though.
Thanks for the codes. Ewald Bleiziffer said in his post he’s actually done it. I’m hoping he’ll provide a link to his work. If not, I’ll try and adapt your code–with citations for your work, of course.
Hi Bradley,
first of all thank you for posting this helpful work.
I want to use it for displaying a network diagram.
To do this I need to add some extra functionality. First I want to add a text to each node, the name of the node. Have you made something similar before or have an idea how to do this?
The second part is to add a ToolTip to each node. The problem where I stuck here, is that I need the absolute Position of each node to compare it with the current cursor position.
Is there a way to get the current absolute position of each node?
Adding text to nodes is quite simple; just create a subclass of Node and override the DrawNode method.
In order implement a ToolTip, you will need an additional method for determining if there is a node under the mouse pointer, e.g.:
public Node HitTest(Point location, Rectangle bounds) { Point center = new Point(bounds.X + (bounds.Width / 2), bounds.Y + (bounds.Height / 2)); // determine the scaling factor Rectangle logicalBounds = GetDiagramBounds(); double scale = 1; if (logicalBounds.Width > logicalBounds.Height) { if (logicalBounds.Width != 0) scale = (double)Math.Min(bounds.Width, bounds.Height) / (double)logicalBounds.Width; } else { if (logicalBounds.Height != 0) scale = (double)Math.Min(bounds.Width, bounds.Height) / (double)logicalBounds.Height; } // then draw all of the nodes foreach (Node node in mNodes) { Point destination = ScalePoint(node.Location, scale); Size nodeSize = node.Size; Rectangle nodeBounds = new Rectangle(center.X + destination.X - (nodeSize.Width / 2), center.Y + destination.Y - (nodeSize.Height / 2), nodeSize.Width, nodeSize.Height); if (nodeBounds.Contains(location)) return node; } return null; }Note that the above assumes ‘location’ is relative to ‘bounds’ and that these are the same dimensions that are passed to the Draw() method. You can call the HitTest() method from the handlers for the mouse events on your form (or whichever control you draw the diagram on). The method will return a Node if there is one at the specified location, otherwise it will return null.
Hi Bradley,
thank you for this very helpful answer.
Now I managed to do all the things I wanted to do.
Really nice work you have done here and good starting point to draw diagrams.
Thank you again for posting this solution.
Hi Bradley ,
Could you provide us how to add text to node , i did it as you reply to Markus ( via overriding the drawnode method , but it redraw the network again
Hi Xander,
The code below provides a very basic example of how to draw text on a node. Note that the text is not taken into consideration when positioning the nodes – to do this, you would also need to override the Size property.
public class TextNode : SpotNode { public string Text { get; set; } public TextNode(string text, Color color) : base(color) { Text = text ?? String.Empty; } public override void DrawNode(Graphics graphics, Rectangle bounds) { base.DrawNode(graphics, bounds); graphics.DrawString(Text, SystemFonts.DefaultFont, Fill, new PointF(bounds.Right + 3, bounds.Top)); } }Pingback: Building a Better Tag Cloud | Brad Smith's Coding Blog
Hi ,
I am porting this code portion into c++.
I have one doubt regarding this bearing angle calculation.
Simply finding the bearing angle is ok.
But why do some other calculation depending on the the difference between x and difference between y?
Please help me.
The ‘tanh’ function only works for values in the range (-1, 1) so the part of the code you’re referring to keeps the input within those bounds. It checks whether the distance in the X direction is smaller than the distance in the Y direction and, if so, swaps the values and calculates the complement of the angle instead – this needs to be corrected before the method returns.
I later discovered that if you replace the ‘tanh’ function with ‘atan2’, you do not need to perform this correction, i.e.
private double GetBearingAngle(Point start, Point end) {
Point half = new Point(start.X + ((end.X - start.X) / 2), start.Y + ((end.Y - start.Y) / 2));
double diffX = (double)(half.X - start.X);
double diffY = (double)(half.Y - start.Y);
if (diffY != 0)
return Math.Atan2(diffY, diffX) * (180.0 / Math.PI);
else
return (diffX < 0) ? 180.0 : 0.0; }
Hello,
Thank you for posting the code – amazing work :).
I have for you a question – I notice that the number of nodes is always random – can I have a way to make a large number of nodes(like 338)?
I also need to make a minimal intersections of the graph edges – Do you have idea how to do that?
Thank you for help – and again , nice job.
The example app I included with the code is just for demonstration purposes – when you use the classes in your own app, you can create as many or as few nodes as you like.
Generally speaking, the interaction between the forces should inherently act to limit the number of intersections – but depending on the topology of the diagram, you might still get a few. Often, the easiest way to deal with this is to just re-run the layout algorithm until you get something you are happy with – or run it a finite number of times and evaluate the best solution; it’s quite straightforward to check for intersecting lines in code.
Thanks man for the implementation. I used it in my engineering graduate project but with some changes. As my project is taking data from twitter and creating graph structures from it (users are nodes and tweets between two people is an edge) I changed the structure. For drawing I used Drawing.Common that is a simillar library to that of winforms. My graphs were not really trees and I needed to add repulsion force range so clusters of nodes would not throw single nodes to the moon 😛 Also I changed initial random positions with range depending on number of nodes which really helped with readibility after layouting. Also if you create graphics from bitmap with high resolution (I used width 16000 and height 8000) and low pixel memory allocation you can create readable graphs with 1000+ nodes. Ofcourse I added your copyright as I modified your idea.
I am reviving what may be considered a zombie discussion. However, I am working on a project that is extending a UML diagramming project (Pyut) that handles Python, Java, and DTDs. I have always been interested in various methods that know how to lay out UML diagrams. I inherited a Sugiyama layout mechanism and adapted my inherited code to know how to do Orthogonal Layouts. This discussion is some very clear code and documentation that with careful study illustrates force directed layouts.
I took the time to port the code to Python while using my beginner knowledge of C# and Windows Forms to know where to put in emulation classes to get some functional code. Additionally, I used the time to study my reference manual Beginning Math and Physics to ensure via unit tests that I implemented as correctly as possible the mathematical computations that Brad provided.
Thanks a lot
See
Python and wxPython implementation
https://github.com/hasii2011/pyfdl
https://github.com/hasii2011/pyut
https://www.oreilly.com/library/view/beginning-math-and/0735713901/
Thanks for letting me know about your port – always exciting to see my code finding new uses. Your support is greatly appreciated.